Advanced Topics

This worksheet is also available in PDF format.

This worksheet makes use of several examples programs that are all available for download from this website.

Array Functions

FORTRAN provides a number of intrinsic functions that are useful for working with arrays. Among these are some which are specifically aimed at working with matrices and vectors.

Function name	Operates on	Description
MATMUL	Matrix/vector	Matrix multiplication of two matrices or a matrix and a vector.
DOT_PRODUCT	Vector	Scalar (dot) product of two vectors
TRANSPOSE	Matrix	Transpose of a matrix
MAXVAL	Any array	Maximum value of an array, or of all the elements along a specified dimension of an array.
MINVAL	Any array	Minimum value of an array, or of all the elements along a specified dimension of an array.
SUM	Any array	Sum of all the elements of an array, or of all the elements along a specified dimension of an array.

Program   matrixmul.f95, demonstrates the use of these functions. Additionally, it includes two subroutines that are likely to be useful when handling matrix/array manipulations: fill_array  which fills the array elements and outputra which prints the values of the array elements to the screen. This program is also an example of dynamic memory allocation.

  program matrixmul
  !demonstrates use of matmul array function and dynamic  
  !allocation of array
  real,  allocatable, dimension(:,:) :: ra1,ra2,ra3
  integer :: size
  !initialize the arrays
  print*, 'Shows array  manipulation using SQUARE arrays.'
  print*, 'Allocate the  space for the array at run time.'
  print*, 'Enter the  size of your array'
  read *, size
  allocate(ra1(size,size),ra2(size,size),ra3(size,size))
  print*, 'enter matrix  elements for ra1 row by row'
  call  fill_array(size,ra1)
  print*, 'enter matrix  elements for ra2 row by row'
  call  fill_array(size,ra2)
  !echo the arrays
  print *,'ra1'
  call  outputra(size,ra1)
  print *,'ra2'
  call  outputra(size,ra2)
  !demonstrate the use of matmul and transpose intrinsic !functions
  ra3=matmul(ra1,ra2)
  print *,'matmul of  ra1 and ra2'    
  call  outputra(size,ra3)
  ra3=transpose(ra1)
  print *,'transpose of  ra1'
  call  outputra(size,ra3)
  deallocate(ra1,ra2,ra3)
  end program matrixmul
  !---------------------------------------------------------
  subroutine  outputra(size,ra)
  implicit none
  !will output a real square array nicely
  integer                               :: size,row,col
  real,dimension(size,size)             :: ra
  character                             :: reply*1
  do row =1,size
     write(*,10) (ra(row,col),col=1,size)   
     10    format(100f10.2)
     !as we don't know how many numbers are to be output, 
     !specify  !more than we need - the rest are ignored
  end do
  print*,'__________________________________________________'
  print*,'Hit a key and  press enter to continue'
  read *,reply
  end subroutine  outputra
  !---------------------------------------------------------
  subroutine  fill_array(size,ra)
  implicit none                         
  !fills the array by prompting from keyboard
  integer        :: row,col,size
  real           :: num
  real, dimension(size,size) :: ra
  do row=1,size
     do col=1,size
       print *, row,col
       read *,num
       ra(row,col)=num
     end do
  end do
  end subroutine  fill_array          

Exercise 7.1

Write a program to read in 2 square matrices (of any size). Confirm that the matrices obey the rule

       (AB)T     =   BTAT

where     A^T         is the transpose of matrix A.

Exercise 7.2

Write a program that will read a 3 X 3 matrix from a data file. In the program, include a subroutine that will generate any cofactor cof of the matrix mat. Call the subroutine cofactor and use these arguments:

  	subroutine cofactor(i,j,mat,cof)
  	implicit none
  	real :: mat(3,3),minor(2,2),cof
  	integer :: elrow,elcol
  	! cof – the cofactor of matrix mat for element i,j
  	.
  	.

Exercise 7.3

Use the program you developed Exercise 7.2 to calculate the determinant  of a 3 X 3 matrix.

Writing REAL programs - Flow Charts

Now that you know all the main elements of FORTRAN 95, you are in a position to apply your skills to writing REAL programs. Unlike most of the exercises in these worksheets, REAL programs tend to be rather large. In large programs, the underlying logic can often be difficult to follow.

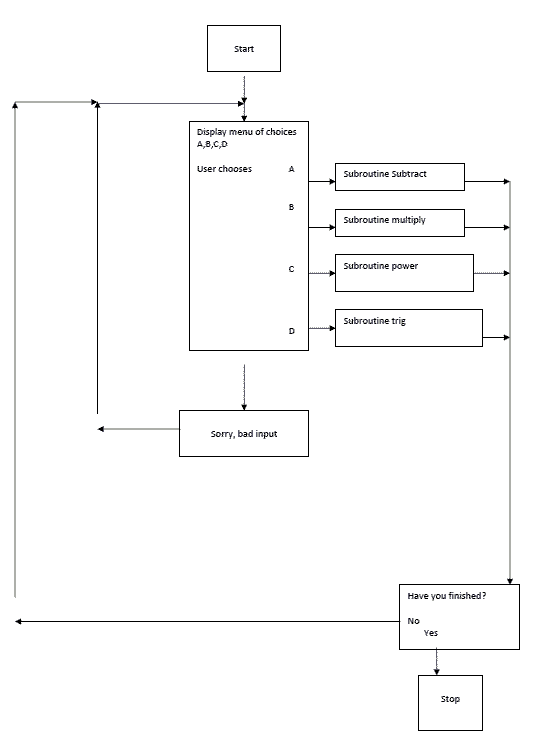
It helps, therefore, both in the devising of a program and later in its maintenance, to have a plan of what you intend the program to do. Let’s take, as an example, a program that works like a calculator.

The flowchart is shown on the next page. The logic of the program, as a whole, is clear. Details like what will happen in the subroutines is glossed over at this stage.

In commercial programming, flowcharts are usually formalized, with specific shapes for boxes that do different things. That need not concern us here. Essentially, we use flowcharts to provide a ‘map’ of the underlying logic flow in the program – what connects with what.