Making Decisions
This worksheet is also available in PDF format.
This worksheet makes use of several examples programs that are all available for download from this website.
Aims
By the end of this worksheet, you will be able to:
- Do arithmetic
- Start to use FORTRAN intrinsic functions
- Begin to understand program flow and logic
- Know how to test for zero – important!
- Learn more about good programming style
Assignment
When we start programming, the similarity between mathematical equations and FORTRAN statements can be confusing.
Consider the following FORTRAN statements:
x = 2 Store the value 2 in memory location x
y = 3 Store the value 3 in memory location y
z = x + y Add the values stored in memory location
x and y and store the result
in memory location z
In mathematics, “x = 2” means that the variable x is equal to 2. In FORTRAN it means “store the value 2 in the memory location that we have given the name x”.
The significance of this is made clearer by the following equation in mathematics:
x + y =z
In mathematics, this means that the left hand side of the equation is equal to the right hand side.
In FORTRAN, this expression is meaningless: there is no memory location "x+y" and so it would lead to a compiler error.
Rule – there can only ever be ONE variable name on the left hand side of an equals sign
Exercise 2.1
Write a program which reads in two numbers a and b. Get the program to swap the values around so that the value that was in a is now in b, and print out the result. Hint you need to declare a third variable for intermediate storage of the data. (Check your program by examining program swap.f95 at Downloads
Arithmetic
The arithmetic operators are
+,- plus and minus *,/ multiply and divide ** exponentiation (raise to the power) () brackets
- The order of precedence in FORTRAN is identical to that of mathematics.
- Unlike algebra, the operator must always be present xy is not the same as x*y
- Where operations are of equal precedence they are evaluated left to right
- Consecutive exponentiations are evaluated right to left
- We can override the order of evaluation by use of brackets
Exercise 2.2
The following program is an example of the use of arithmetic.
program calculate implicit none ! a simple calculator real :: x,y,z,answer x=1.5 y=2.5 z=3.5 answer=x+y/z print *,'result is ',answer end program calculate
Explore the use of arithmetic operators by modifying program calculate. Use it to calculate the values:
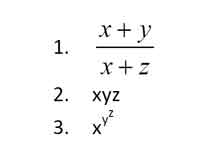
Intrinsic Functions
FORTRAN is especially useful for mathematical computation because of its rich library of inbuilt functions (intrinsic functions). We shall mention a few briefly here:
| function name | type of argument | type of result | Definition |
|---|---|---|---|
| sin(x) | real | real | sine |
| cos(x) | real | real | cosine |
| tan(x) | real | real | tangent |
| atan(x) | real | real | arctangent |
| abs(x) | real/integer | real/integer | absolute value |
| sqrt(x) | real | real | square root |
| exp(x) | real | real | ex |
| log10(x) | real | real | log10x |
Trigonometric functions are calculated in radians (1 radian = 180/Pi degrees).
There are, of course, many more, and this list doesn't cover all FORTRAN variable types. The following example shows the use of some of the inbuilt functions.
program trig implicit none real :: a,pi print *,'Enter an angle between 0 and 90' read *, a pi = 4.0*atan(1.0) print *,'the sine of ',a,' is ',sin(a*pi/180) end program trig
Making Decisions
So far, our programs have worked as little more than basic calculators. The power of programming comes in when we have to make decisions. Copy the example program, test.f95, to your own file space. See if you can understand what is going on.
program test
implicit none
!use of a simple menu
real :: x,y,answer
integer :: choice
!set up the menu – the user may enter 1, 2 or 3
print *,'Choose an option'
print *,'1 Multiply'
print *,'2 Divide'
print *,'3 Add'
read *,choice
x=3.4
y=2.9
!the following line has 2 consecutive
!equals signs – (no spaces in between)
if (choice == 1) then
answer=x*y
print *,'result = ',answer
end if
if (choice == 2) then
answer=x/y
print *,'result = ',answer
end if
if (choice == 3) then
answer=x+y
print *,'result = ',answer
end if
end program test
The highlighted lines in the above program are called if … end if statements. They work like this:
if (condition is true) then execute this line and this and so on until we get to … end if
It follows that if the condition is NOT true then the code 'jumps' to the next statement following the 'end if'. The statements between the if and the end if are deliberately indented, this makes the program easier to read.
We use two consecutive equals signs (no space in the middle) to test for equality. Compare:
if (choice == 3) then test
choice = 3 assignment
Exercise 2.3
Examine program test above. The line:
print *,'result = ',answer
is repeated several times. Is this a good idea? Can you modify the program to make it more efficient?
Program Style
A good program:
- Uses comments appropriately to explain what is happening.
- Uses indentation to make the program easier to read.
- Uses meaningful variable names.
- Uses sensible prompts to let the user know what is going on.
- Uses implicit none at the start of every program.
- Is efficient!
If you want to get maximum marks for your assignments keep the above points firmly in mind. It is not enough just to get a program to work!
More on decision making
In our test.f95 above, there was a problem if the user entered a value that wasn't catered for by the program.
What happens if the user doesn't enter one of the values 1, 2 or 3?
We are going to look at a new structure, called if, else, endif that handles this situation. Examine the following code snippet:
if (choice = = 1) then
do something
else if (choice = =2) then
do something else
else
do this if nothing else satisfies the conditions
end if
Other logical operators
So far, all our tests have been for equality. In fact, there are several tests we can make:
== equal to (there is no space between the equals signs) /= not equal to < less than <= less than or equal to > greater than >= greater than or equal to
Multiple Conditions
Suppose we need to test if x is greater than y and y is greater than z. There are different ways of doing this:
if (x > y) then if (y > z) then do something end if end if
This can also be handled by the following:
notice the .and.
if (x > y .and. y > z) then do something end if
If we wanted to check whether a number were less than a given value or greater than a given value we could write:
notice the .or.
if (x < 10 .or. x > 20) then do something
end if
Exercise 2.4
Write a program that reads a number from the keyboard. Get the program to decide whether:
- the value of the number is greater than 0 but less than 1
- or is greater than 1 but less than 10
- or is outside of both these ranges
Print out a suitable message to inform the user.
The simple if statement
There is a simpler, one line form of the if statement. Say we just wanted to print out a simple message such as
print *, 'enter a positive number' read *, num if (num <0) stop if (num < 10) print *, 'less than 10' if (num > 10) print *, 'greater than 10' print *,'It is a positive number'
This snippet also introduces a useful, simple statement stop – it simply stops the program.
Important note – testing for zero
Suppose that you wish to test whether a real variable is zero. The test
if (x == 0) then ….
is not a satisfactory test. Although integer numbers are held exactly by the computer, real numbers are not.
The way around this is to test if the absolute value of the variable is less than some small predefined value. For example:
if (abs(x) < .000001) then print *,’No zero values! Please enter another number’ read *, x end if
