Files and Precision

This worksheet is also available in PDF format.

This worksheet makes use of several examples programs that are all available for download from this website.

Reading from files

In the real world, most of the data we use for our programs will be kept in files. We just need a modification to the read  statement that we are already familiar with to do this.

This program reads 3 numbers from a file called 'mydata.txt' into an array. Use Windows Notepad to create such a file for yourself, or copy the file from mydata.txt which is on the website.

        program readdata
        implicit none
        !reads data from a file called mydata.txt
        real :: x,y,z
        open(10,file='mydata.txt')
                read(10,*) x,y,z
        print *,x,y,z
        end program  readdata   

The new material here are the lines

        open(10,file='mydata.txt')
        read(10,*) x,y,z

The open statement links the file called 'mydata.txt' with an input device numbered 10 (it doesn't have to be 10, it could be any positive integer). To read from device 10, we just use it as the first argument in the read statement.

Exercise 4.1

Use Notepad to create a  file called evenodd.txt. In the file type 10 numbers, one per line. Write a program that reads data from evenodd.txt one line at a time. Check if each number is even or odd and print out a suitable message. One way to check if a number is even or odd is to use the mod intrinsic function, like this…

                if (mod(num,2)>0) then……

mod returns the remainder of the first argument divided by the second. If the return value is greater than zero, then the number must be odd.  Check program evenodd.f95 to see if you are correct.

Writing to files

This is a similar idea to reading from files. We need a new statement, though, instead of print, we use write.

        program io2
        !illustrates  writing arrays to files
        implicit none
        real :: num
        integer :: i
            open(12,file='myoutput')
        do i = 1,100
        num = i/3.0 
            write(12,*) num
        end do
        print *, 'finished'
        end program io2

Exercise 4.2

Write a program which reads in numbers from a file one at a time. If the number is positive, it should  store it in a file called 'positive.txt' and negative numbers in a file called 'negative.txt'.

Extending the precision

So far, we have used two types of variables, real and integer. The problem so far, as you will have noticed on output, is that we are extremely limited by the number of significant digits that are available for computation. Clearly, when we are dealing with iterative processes, this will lead rapidly to errors. We can, however, extend the precision available from the single precision default, which gives us 6 figure decimal precision to 15 figures by using a new specification for real numbers.

        program extended
        implicit none
        integer, parameter  :: ikind=selected_real_kind(p=15)
        real (kind=ikind)  :: sum,x
        integer :: i
        sum=0.0
        do i=1,100
          x=i
          sum = sum +  1.0/(x**6)
        end do
        print *, sum
        end program  extended     
        

produces the following output:

        1.01734306196

Don't be put off by the odd looking code. In practice, the way of setting up this extended precision, is pretty much the same for every program.

We state the precision we want by the argument p

        
        integer, parameter ::  ikind=selected_real_kind(p=15)

in this case, 15 decimal places. ikind is a new data type – a parameter. FORTRAN returns a value to the parameter ikind that will be adequate to provide 15 digit precision. This code will work on any machine irrespective of the architecture. 

We declare that the variables are using extended precision by

        real (kind=ikind) ::  sum,x

Valid values for p are 6, 15 and 18. The default value for p is 6. If you ask for more precision than 18 digits, the compiler will complain with an error message.  Try changing the values of  p and see what effect this has on the output.

The trouble with PRINT is that the programmer has no control over the number of digits output irrespective of the selected precision .

Later on we'll come back to this when we learn about the WRITE statement, and output formatting.

Note Unlike variables, parameters may not change once they are declared.

If we want to use constants in a program that uses extended precision, we have to tell FORTRAN that they are also extended precision explicitly. This leads to the rather strange syntax you can see in the following program.  

   program extendedconstants
  !demonstrates use of extended precision 
  implicit none
  integer, parameter ::  ikind=selected_real_kind(p=18)
  real (kind=ikind) :: val,x,y
  val=10/3
  print*,val                  !10/3 calculated as  integer  - wrong!
  x=10.0
  y=3.0
  val=x/y              !x/y assigned to extended  precision - right!
  print*,val
  val=10.0_ikind/3              !extend precision constant -  right!
  print*,val
  val=10.0/3.0                              !real constants - wrong!
  print*,val
  val = .12345678901234567890               !real constants - wrong!
  print *, val
  val = .12345678901234567890_ikind   !ext precision consts - right!
  print *, val
  end program  extendedconstants    

You should run this program for yourself and think carefully about its implications. This program demonstrates how easy it is to get calculations wrong.  I’ll leave this to you to experiment to ensure that you fully understand the importance of properly declaring variables and the use of constants in FORTRAN programming. A systematic approach to your programming will reduce the risk of errors as will running programs with test data that have known solutions so that you can confirm that your program is error free.

Magnitude limitations

We have already observed that there is a limitation of the accuracy with which we can do calculations in FORTRAN (and indeed, any, computer language). There are also limitations on the magnitude of a number. The various magnitude and precision limits are summarized in the following table:

Exercise 5.3

To illustrate these limits copy file  magnitude.f95  and run the program. Take a while to get a feel for what is going on. Try inputting various values for the variable maxpower (eg 400). Can you confirm that the table above is correct?

One interesting construct is

	print *,i,2.0_ikind**i

Here, we are telling the compiler that the real constant 2.0 is also using extended precision. Check what happens if you select extended precision (option 3) and enter a value of maxpower of 400. See what happens  if you rewrite the line to be

	print *,i,2.0**i

Run the program again and enter the same values. Can you explain what is going on?

Convergence – exiting loops  on a condition

In the program extended.f95, we found the sum of

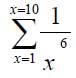
It is useful to determine at what point such sums converge to a steady value – otherwise we may make arbitrary assumptions about the summation range. Clearly, a point will be reached, within the precision range that can be handled on our computer, that the term

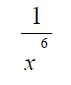
will be too small to contribute to the sum. At this point we should exit the loop otherwise the program will do more computation than is required.

One way to do this is to compare the value of the variable sum with its previous value, and if the difference between the two is very small, then exit the loop.

  program  whileloop
  implicit none
  integer, parameter ::  ikind=selected_real_kind(p=15)
  real (kind=ikind) ::  sum,previoussum,x,smallnumber,error
  integer :: i
  sum = 0.0
  previoussum = 0.0
  smallnumber = 10.0_ikind**(-15.0)
  do i=1,1000
     x=i
     sum = sum + 1.0 /(x**6)
     error=abs(sum-previoussum)
     if  (error<smallnumber) then
         print *,'sum  ',sum,' number of loops ',i
         exit
      end if
     previoussum = sum
  end do
  end program  whileloop

It is not necessary  to always use a loop counter in a do loop.  If we don't actually specify a counter, the program will loop forever. Constructs like this are OK:

  	smallnumber = .0000001_ikind
  	do
  	print *, 'enter a  positive number '
  	read *, number
  		if (number <=  smallnumber) exit 
  	end do
  

The disadvantage is that, if you get the code wrong, you run the risk of the program looping forever – generally it's safer to use a loop counter!